The Power of Recursion: Visualizing Fractals with Code

We come across patterns and symmetry all around us in our daily life. Every symmetry has some maths inside it. Recursion helps us discover the core essence of a pattern and reflect it into code — making the computer do all the calculations and produce something beautiful.

Recursion is just doing something over and over again with slight modifications.

A Simple Example

Let’s take a circle.

We draw another circle half the diameter of the previous one until the diameter becomes 1.

The end condition is important — otherwise, the recursion will never stop (though modern computers eventually stop it due to stack limits).

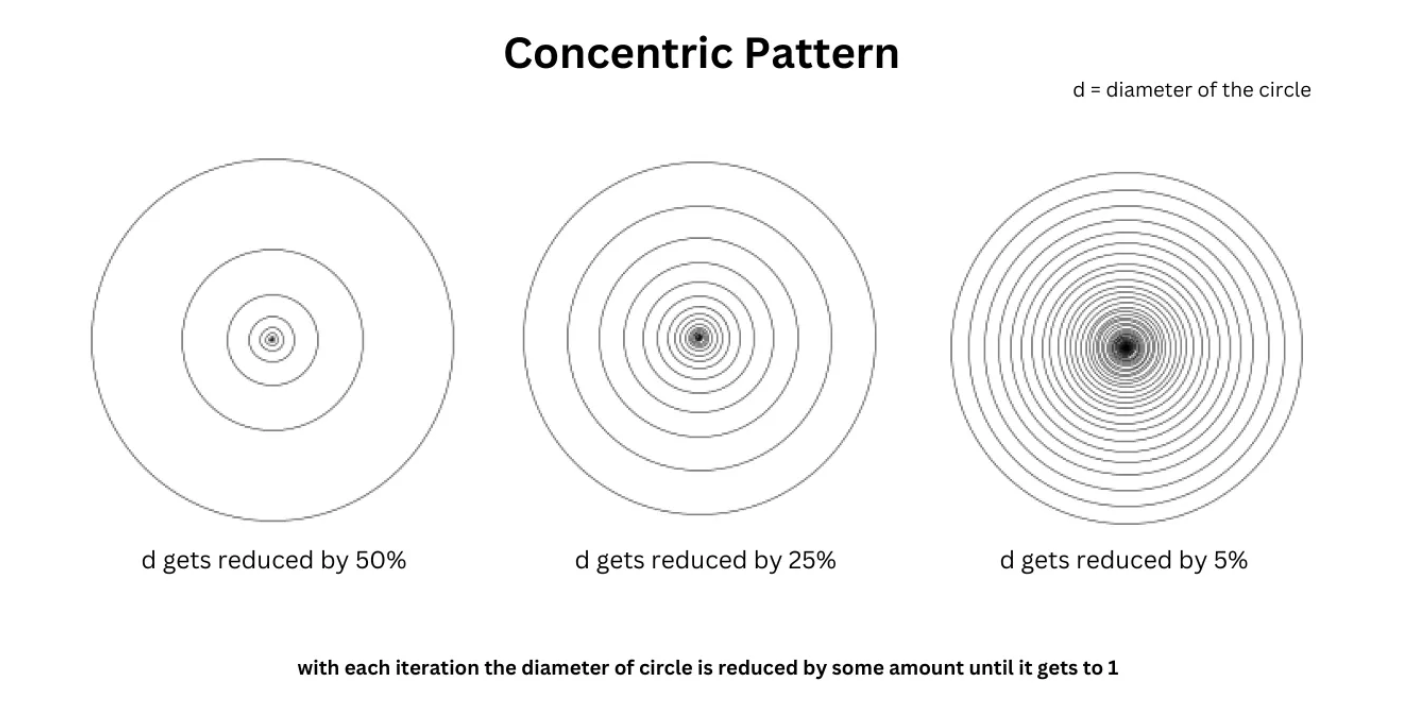
These patterns are computer-generated using a very simple recursive function:

void drawCircle(float x, float y, float d) {
    noFill(); 
    strokeWeight(1);
    circle(x, y, d);  // draws a circle at x, y with diameter d
  
    if (d < 1) return;  // condition to stop the recursion
 
    drawCircle(x, y, 0.50 * d); // calls itself with d = d/2
}

Adding Some Movement

Now let’s do something more interesting.

Instead of drawing the next circle at the same position, let’s move the X position:

x = x + d/2 and d = d/2

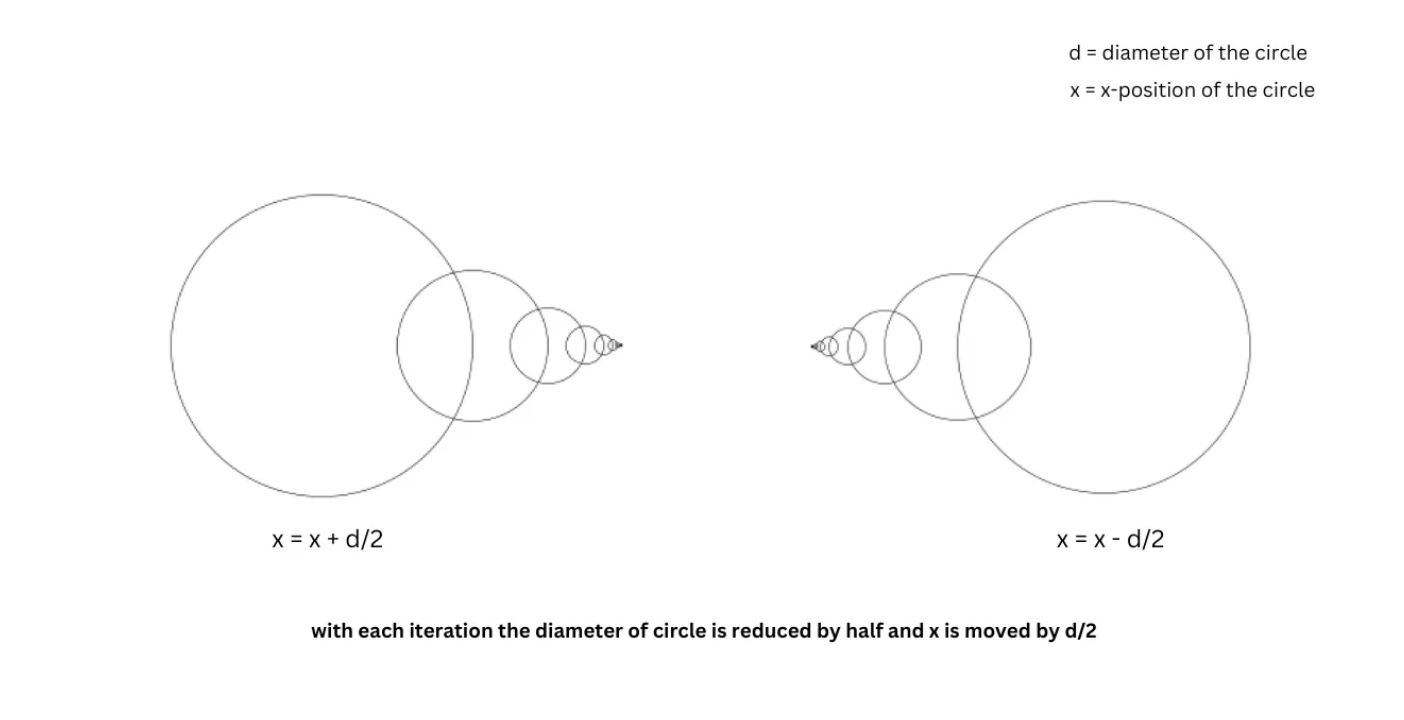
Moving in Both Directions

We can extend this idea to the Y direction as well:

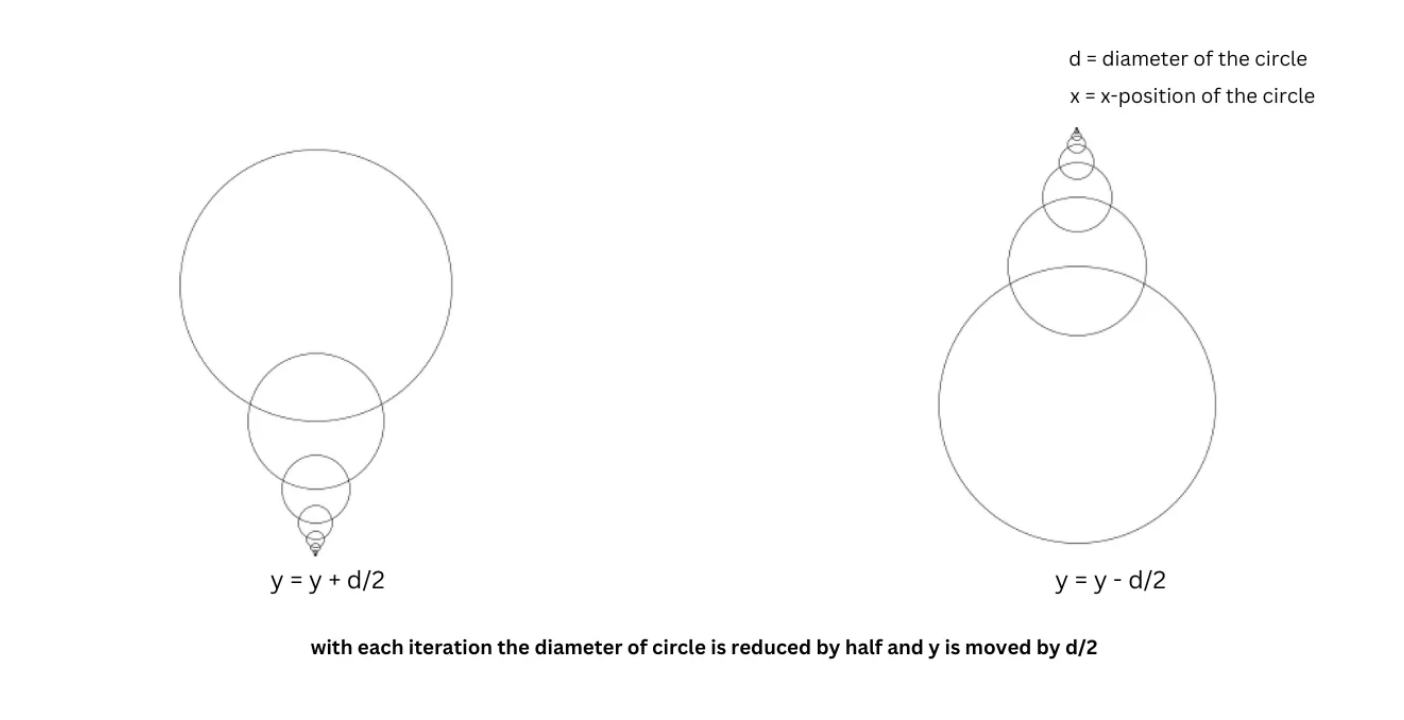
Combining Transformations

Now things get fun.

Let’s combine:

• x = x + d/2
• x = x - d/2

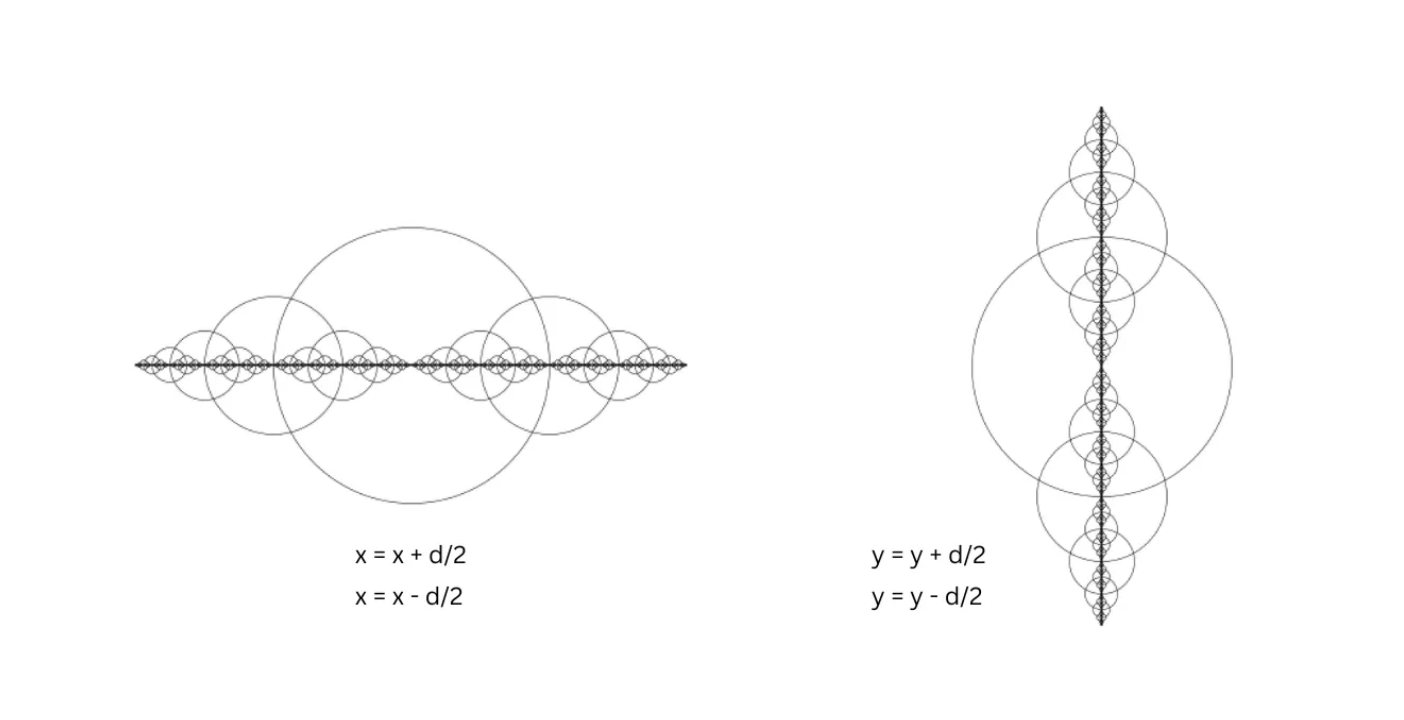
How cool is that?

Obviously, this level of precision is beyond human capability — computers are extremely good at repeating patterns perfectly.

The Fun Part: Emergence of a Fractal

Now let’s combine:

• Both X transformations
• One Y transformation

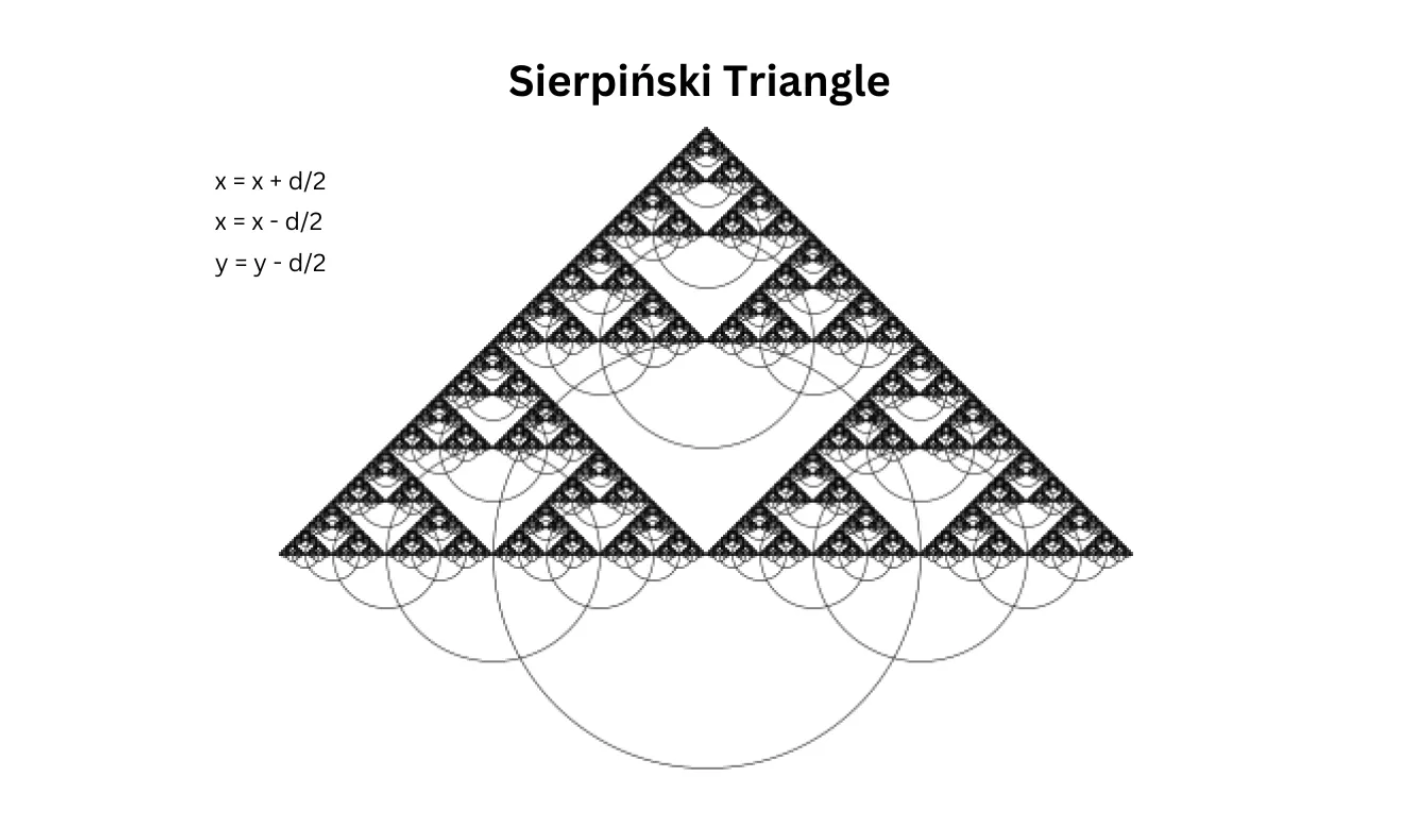
🎉 Congratulations! You’ve just created a Sierpinski Triangle.

What Is the Sierpinski Triangle?

The Sierpinski Triangle is a self-similar fractal. It consists of an equilateral triangle, with smaller equilateral triangles recursively removed from its remaining area.

It is named after the Polish mathematician Wacław Sierpiński.

The Code

Here is the code for the above figure:

void drawCircle(float x, float y, float d) {
    noFill();
    circle(x, y, d);
    strokeWeight(0.5);
 
    if (d < 1) return;
 
    drawCircle(x + d/2, y, d/2);
    drawCircle(x - d/2, y, d/2);
    drawCircle(x, y - d/2, d/2);
    // drawCircle(x, y + d/2, d/2);
}

Try It Yourself

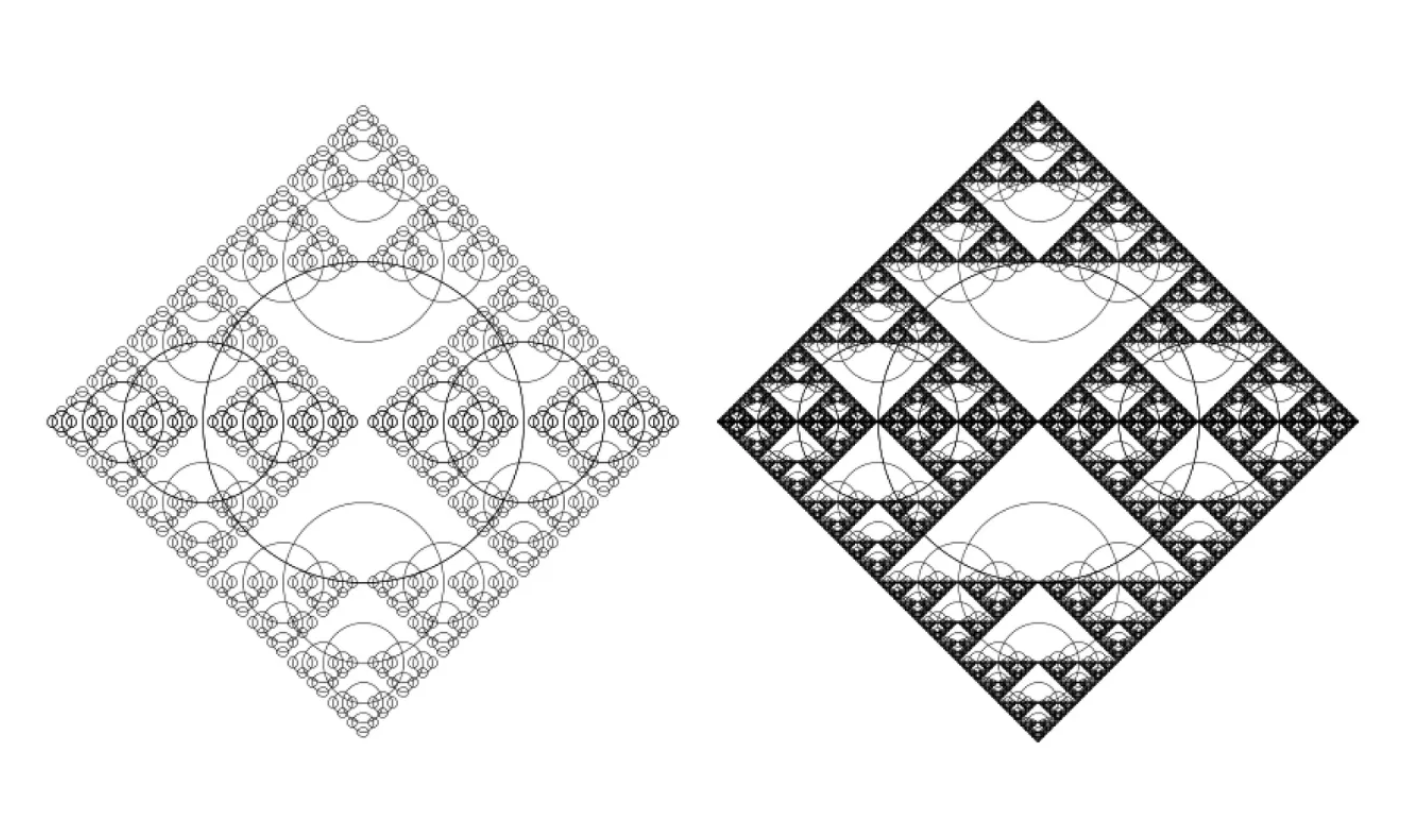
From this point onward, you can:

• Tweak additions & subtractions
• Change multipliers and divisors
• Modify termination conditions

Every time, you’ll get a completely different pattern.

Final Thoughts

Achieving this through computation took years of technological advancements. Computers can do far more sophisticated things — this is just the tip of the iceberg.

If this felt interesting, consider following me. That motivates me to write more such articles 🙂

If you want to know:

• Which language this is
• Which environment was used
• Or want more examples

Leave a comment and I’ll write a follow-up article.

See you next time! 🚀